Vetka Puzzle

Rules Of the game

Vetka (the name is transcription of russian word “ветка” which means “tree branch”) is an original puzzle game invented by GAMOS. It is played on a square field divided into square cells. In the course of the game fragments can not be moved from their initial locations but only rotated within their cells. The purpose is to reconstruct a connected single-piece structure without loops.

Original game from GAMOS (see http://www.gamos.ru/eng/games/branch.htm) features nice tileset, animation, timekeeping, scoretable and other small features which make a game a game. GAMOS also sells very similar game NetWalk.

Customization

In a customizable version of the game you can choose field size, different tileset and also allow generation of the structures with a “+”-shaped tile.

Uniqueness of the solution

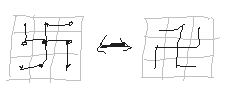Is the solution unique? My first guess was “of course not”. I thought there are many ways to rotate tiles to end up with different trees. For example swastika shaped tree (3x3) allows 2 different assemblies. But after playing several games I found out that all of them had unique solution, especially those that did not have “+” shaped tile in it. I tried to build 2 different trees which differ only by rotations of some tiles and does not contain “+” shaped tiles, but failed.

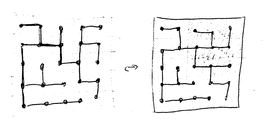So, my second guess was that such trees can be reconstructed in a unique way. Then I tried to prove this and was trying to until one day computer generated a puzzle for me that allowed 2 different solutions. 8 tiles in upper right corner can be rotated to produce different tree. This tree can be reduced to 4x4 tree, which leaves me with a question: what is the smallest possible tree (with no “+” tiles) that allows 2 solutions? Is there such 3x3 tree? 3x4?

I programmed this puzzle during the period when I believed my second guess is correct. As a result I detect end of game in the following way: I generate tree and then I keep count on the number of turns for each tile. (Scrambling is done by performing random number of turns on each tile.) I assume that tree is reconsructed when each tile returns to its original position. This leads to unfortunate consequences that one day you will build a tree and this will not be detected by the program. This means that you were extremely lucky and found a tree which allows at least two solutions and you've just found “another” one.

Variants

On its highest difficulty level original game from GAMOS can be played on a toroidal field (I haven't implemented this variant). It definitely adds to difficulty. Original variant also does not fill the entire game field with tiles. It is hard to say, if this makes puzzle more difficult or not, but it produces more visually appealing image of a completed puzzle.

Another obvious variant is to use hexagonal tiles instead of square ones. This one I have implemented. I call it Vetka6X. It is more difficult than original Vetka. I do not know if there are any commercial implementetions of this puzzle.

There is one more tileset that covers the plane -- triangles. My original estimate is that since there are only 4 types of tiles and this includes empty tile and Y-shaped tile (both of which are not affected by rotations), this variant will not be very challenging. But I will definitely try to implement it one day and check this hypothesis.

Plane can be tiled by regular polygons only in three different ways, so, no more variants of this type are possible. However, if we move from regular euclidean plane to non-euclidean plane, we arrive to infinity of possibilities. Non-euclidean plane allows infinitely many tilings by regular polygons, giving infinitely many variants of Vetka puzzle. Creating user interface for displaying and manipulating figures in non-euclidean plane is a challenge. It is not impossible and there are implemetations with usefull applications (lookup “Hyperbolic Tree” with your favorite search engine for an example).

Author

The game was programmed in Javascript by Andrew Nikitin.

[ Index page | Feedback ]