I tried to modify my program so it would search for unfoldings of another platonic solid. Tetrahedron was too trivial, Icosahedron was beyond possibilities of that program (executed on Z80 microprocessor), so octahedron was a natural choice. To my utter surprise the program came out with the same number -- 11.
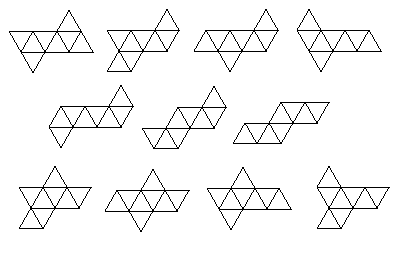
Indeed, since cube is dual to octahedron, each unfolding of a cube corresponds to a unique unfolding of octahedron. Edges of solids correspond to each other and cut edge of a cube unfolding corresponds to uncut edge of octahedron unfolding and vice versa. Same is true for any pair of dual polyhedra (with properly defined notion of unfolding, to allow self-intersection).
http://mathworld.wolfram.com/Net.html mentions this fact. It also lists 43380 as number of unfoldings for icosahedron.