Cube to tetrahedron

Puzzle

Cut cube in two pieces from which tetrahedron can be assembled.

Solution

The third Hilbert problem states "Can solid tetrahedron be cut into finite number of pieces from which cube can be assembled?". The answer to this problem was found by Max Dehn a few months after the problem was stated (in fact, this was the first solved Hilbert problem) and this answer was negative. Dehn proved that it is impossible.

This puzzle does not ask you to solve impossible problem. Instead it asks if surface of solid cube can be cut in to pieces, which then can be unfolded into plane, rearranged and folded back into tetrahedron.

Cut cube along some edges and unfold it into the following figure. (It can be folded back into a cube along black dashed lines.)

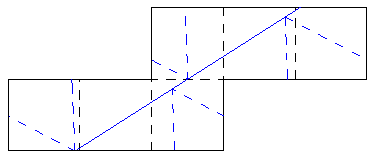
If you cut it along solid blue line and rearrange parts as this

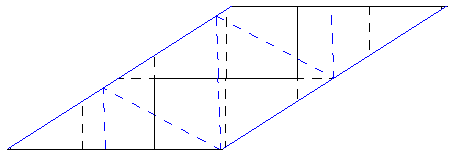
the resulting parallelogram can be folded into tetrahedron along blue dashed lines.

Improvements

Can number of pieces be further reduced? Down to 1? At first it may sound crazy, but maybe, it is possible to come up with unfolding that can be folded into both cube and tetrahedron. There certainly exists a polygon that can be folded both into cube and irregular tetrahedron. If you find common unfolding for cube and regular tetrahedron, please drop me a note.

Possible variants

If we allow immeasurable sets as pieces this porblem might have a solution for solid cube and tetrahedron. After all, when you can cut a solid sphere into 5 pieces from which you can assemble 2 solid spheres of the same radius, then merely turning cube into tetrahedron does not seem implausible. I haven't tried this path, quite possibly, there is a solution there too.

[ Index page | Feedback ]