Polycube unfoldings
Polycubes are solid bodies assembled from several identical cubes so their
faces touch each other. There is one monocube (that is, regular cube), 1 bicube
(two cubes side by side), 2 tricubes
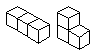
There are also 7 (8 if you want to count 2 mirror
images as diffrent polycubes) tetracubes.

(More on polycubes)
Some unfoldings of these solids can be constructed by using only squares that
touch with their sides. In the following we only consider such unfoldings.
Puzzle 1
How many common unfoldings are there for tricubes?
Puzzle 2
How many common unfoldings are there for tetracubes? You may exclude the 2x2x1
tetracube since it has different surface area then the rest of them, or you may
think of it as "U" shaped solid with infinitely thin slide that cuts along some
pair of touching faces.
In case, there is no unfolding which is common for all tetracubes, what are
unfoldings which are common to some large subset of all tetracubes?
Puzzle 3
Once some of the common unfoldings are found, it becomes a puzzle in itself:
fold given polyminoal shape into as much polycubes as you can.
Here are some examples.
Puzzle 3a. Tricubes 1
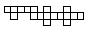
Fold it into both straight and L-shaped tricubes
Puzzle 3b. Tricubes 2
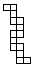
Fold it into both straight and L-shaped tricubes
Puzzle 3c. Tetracubes
How many tetracubes can you fold from this:
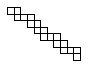
Practical considerations
I tried to make real world puzzle based on this idea. First attempt consisted
of a pattern printed on regular paper, then cut and folded. I found out that
this does not work very well, since paper dos not stay the way you fold it and
you have to keep it together all the time with your fingers.
 Next thing I thought of was several wooden or plastic squares, connected with hinges that lock in 0°, 90°, 180° and 270° positions. Alas, I could not find such hinges in the hardware store -- apparently nobody needs hinges with such feature.
Next thing I thought of was several wooden or plastic squares, connected with hinges that lock in 0°, 90°, 180° and 270° positions. Alas, I could not find such hinges in the hardware store -- apparently nobody needs hinges with such feature.
So, I settled on a paper pattern that I wrap around polycubes built from toy
builder's blocks.
If you have better idea how to make this puzzle, I would love to hear about
it.
[
Index page
|
Feedback
]



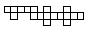
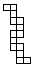
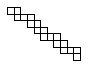
 Next thing I thought of was several wooden or plastic squares, connected with hinges that lock in 0°, 90°, 180° and 270° positions. Alas, I could not find such hinges in the hardware store -- apparently nobody needs hinges with such feature.
Next thing I thought of was several wooden or plastic squares, connected with hinges that lock in 0°, 90°, 180° and 270° positions. Alas, I could not find such hinges in the hardware store -- apparently nobody needs hinges with such feature.