Basic Slide Rule Operations

Setting the values on a scale

Setting of the values comes in tree slightly different varieties:

• moving cursor line to the desired number point on one of the scales (no matter on slide rule body, or on a slide);
• moving the slide, so that desired number point on one of its scales appears under the hairline
• moving slide so, that index mark, either left ('1') or right ('10'), appears over the desired number over the body scale that is adjacent to the slide
• moving slide so, that desired number on a scale adjacent to the body appears over the left or right index of the body scale that is adjacent to the slide

Reading the values from a scale

Basic unary operation

In short notation this is written as |->uU; |=>vV, or, with further simplification: uU=>vV. 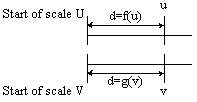This operation allows to perform calculations in the following unusual way:
If we match value u on scale U with formula d=f(u) against v on scale V with formula d=g(v) then, because d is the same for both formulas, u and v are in the following algebraic relationship: f(u)=g(v). This can be interpreted to calculate either

For example, the value u on scale C with formula d = log₁₀x and the vaue v on scale A with formula d = (1/2)*log₁₀x are in relationship log₁₀u = (1/2)*log₁₀v. This relationship can be used to calculate either

If one of the U or V is on body and another is on slide, then these formulas depend on some constant (position of the slide), thus allowing to use slide rule as a function table for the whole family of functions.

Reversing the slide

This actions changes formulas of the scales located on the slide from d = f(u) to d = 1-f(u). In some cases this increases range of function that can be represented by appropriate choice of a pair of slide rule scale.

Unary formula examples

Basic ternary operation

Unlikely, the basic slide rule operation is ternary in nature, that is, it has 3 operands. This operation can be described in the following way: move u on scale U to v on scale V and read the result r from scale R under w on scale W. In short notation this is written as uU->vV; wW=>R(r). In practice, however, you will often be required to use cursor to perform this: |->vV; uU->|; |->wW; |=>R(r). Please note, that operation takes 3 arguments (u, v, w) to produce a result (r).

If U, V, W and R have formulas (respectively) d=f(u), d=g(v), d=h(w), d=t(r) then (see picture) t(r)-g(v) = h(w)-f(u), or

Note, that here R is scale on body, and W is scale on slide. This case is most useful -- since the result obtained on a body scale can often be used in subsequent calculations without reading. However, situation when the result is read from some slide scale is also valid. Referring to the same picture, now r is one of the input parameters and w is a result uU->vV; rR=>W(w) yields w = h^-1(t(r)-g(v)+f(u)).

Important example

Scales C and D are present on every slide rule, that is why this operation is so important.

Reversing the slide

Proof. Indeed, let U, V, W, R have formulas d=f(u), d=g(v), d=h(w), d=t(r) respectively. Then operation (2) yieds formula

Multiplying two numbers