![==[]--](sr.gif) Trigonometry
Trigonometry
![==[]--](sr.gif) Trigonometry
Trigonometry
Sometimes usage of these scales to solve trigonometric problems is straightforward -- direct application of textbook formulas when slide rule serves just as a multiplication aid. But sometimes there are amazing shortcuts specific to slide rule. This page presents some of the latter.
The three definitions of the milBy the way, when angle is measured in degrees, fractions of degrees can be expressed as minutes and seconds, or as regular decimal fractions.There are 2000×π milliradians in a circle. So a milliradian is just over 1/6283 circle. Each of the definitions of mil are similar to that value but are easier to divide into many parts.
- 1/6400 circle in NATO countries.
- 1/6000 circle in the Soviet Union
- 1/6300 circle in Sweden. The Swedish term for this is streck literally "line". Sweden has not been part of NATO or the Warsaw Pact
As a result of such proliferation trig scales may be marked according to all 8 conventions. I haven't seen Swedish mils on a slide rule yet, but have no doubt such slide rules exist.
Another possibility for variation is scale placement. For example, if slide rule has only 2 trigonometric scale (S and T) there are 2 major possibilities: 1) both of them are located on stock and 2) both of them are located on slide. Operations for these 2 cases may differ. So, to distinguish these cases scales will be denoted TD and SD if they are located on the stock (sines/tangents may be read from D scale) and TC and SC if they are located on the slide (sines/tangents may be read from C scale)
Finally, while most of the time trig scales relate to C/D scales, sometimes sine scale relates to A/B.
You need to keep all this in mind when trying to apply algorithms described in this chapter with your slide rule. Emulator provides scales marked in degrees and decimal fractions of a degree, thus all examples have angular quantities expressed in this form. All algorithms so far rely on S and T scales being related to C and D (rather than A and B).
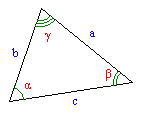 Among all triangle solutions the case of oblique triangle with a given side and 2 angles is the easiest. This is because of sine theorem:
Among all triangle solutions the case of oblique triangle with a given side and 2 angles is the easiest. This is because of sine theorem:
From sinα=a/c and tgα=a/b follows c=a/sin(arctg(a/b)).
John Mosand described corresponding slide rule algorithm on 27-Aug-2000 in slide rule mailing list in the following words (assuming that both S and T scales are located on stock):
![S,T[CI,C]D](sr3.gif) (Try this calculation. Use a=3, b=4 then c should be 5)
(Try this calculation. Use a=3, b=4 then c should be 5)
aC->1DI;bDI=>T(x);xS=>DI(c)
![[S,T,C]DI](sr3.gif) Try with example a=3, b=4 (c=5).
Try with example a=3, b=4 (c=5).
This is equivalent to the previous algorithm because "move slide index to a on DI" puts slide in is exacltly the same position as "move a on scale C to stock index".
The best solution for such layout I've come up with requires 2 slide movements: 1C->bD;|->aD;|=>T(x);xS->|;1C=>D(c).
If you know 1 movement solution, please tell it to me.
... I have found a method of solving quadratic equations in the Mathema Manual. It is called the "Goniometric Solution of Quadratics." For real a,b>0, if x2+2ax-b2=0, define μ by tan(2μ) = b/a, then the roots arex1 = b tan(μ) andx2 = - b cot(μ). ... Also, for x2+2ax+b2=0 and b < a, define μ by sin(2μ) = b/a, then the roots are x1 = - b tan μ and x2 = - b cot μ. For the last quadratic, there are no real solutions if b > a. This approach is perfect for the slide rule. But there is a little difference in application depending on where the tangent scale is and how many T scales are present.
Suppose we have a FC2/83N with T1 and T2 on the stock. For some x, we have x2 + 234x - 5670 = 0. Then a = 234/2 = 117 and b = sqrt(5670) = 75.2.
Since 234 > 0 and -5670 < 0, x1 > 0 and x2 < 0. By estimation we find the decimal points and x1 = 22.1 and x2 = -256.
- Place C1.17 over D7.52.
- Move hairline to C1, read angle T132.7°, 32.7°/2 is 16.4°.
- Move hairline to T116.4° and place C1 under the hairline.
- Move the hairline to CF7.52, read DF2.21.
- Move the hairline to D7.52, read C2.56.
One important point, before we attack ax2 + bx + c = 0, it is prudent to find b2 and 4ac and compare. We don't want to pick up our slide rule and search for roots that aren't there.
Let's solve equation x3 - p*x + q = 0.
Substitution x=k*sin(t) gives
Let k=2*3-1/2*p1/2:
Multiply by 33/2*2-1*p-3/2:
Using formula sin(3*t)=3*sin(t) - 4*sin3(t):
(Generally speaking (*) has 3 solutions with (**) being only one of them: